Do Reliable Predictors Exist for the Outcomes of NASCAR Races?
Introduction
This research attempts to ascertain whether factors known prior to a NASCAR race can help to predict the order of finish of that race. We provide evidence in the form of correlation analysis of the order of finish with available quantitative and categorical information collected, and a simple test for the effect of teams (regressions for each races are also available from the authors). Data were collected on 14 races from the 2003 NASCAR Winston Cup (now Nextel Cup Series) schedule.
Many factors influence the outcomes of NASCAR races. The speed and handling of the car, the skill of the driver, and the performance of the pit crew are but a few of the variables that are important determinants of the finish for a particular car and driver. Many variables outside the control of a particular team, such as the behavior of other drivers, weather, cautions, and the like also influence the final order of finish in NASCAR races. A priori, then, it would be anticipated that predicting outcomes in any meaningful way would be problematical.
The goal of this project is to determine whether those objective, measurable, variables known prior to the start of a race are useful in determining the order of the outcome. To this end we have assembled full data sets for 14 different races from the 2003 NASCAR Winston Cup series. The data include the following for each race: the order of finish, pole position, qualifying speed, practice time, the number of team members of a given driver in the race, the finish position in the prior race at that particular venue, the finish position in the immediately preceding race, driver points for the previous year in Winston Cup competition, and laps completed for the previous year in Winston Cup competition. We also have dummy variables to indicate whether it is the rookie year for a driver and whether the driver changed teams for the current year.
A Simple Model
As a first approach to the problem of predicting the order of finish in particular NASCAR races, we offer a simple theoretical model. Order of finish is posited to be functionally related to variable sets reflecting car speed, driver characteristics, team characteristics, performance in related races, and other factors. In functional notation,
F = f(S, D, T, RR, O), where:
F = Order of finish for a particular race
S = Car speed
D = Driver characteristics
T = Team characteristics
RR = Performance in related races
O = Other factors
To be sure, the variable categories listed are not distinct from each other. That is, empirical measures of car speed are certainly related to other categories of variables such as driver and team characteristics. The theoretical model serves to provide a framework for the empirical specification of the model.
Car Speed, Driver Characteristics, and Related Races
The effects of car speed on race outcomes are obvious. Faster cars will, on average, finish better. Also obvious are the effects of driver racing skill and experience. If it is possible to proxy for driver racing skill and experience, such proxies should be related to finish position across races.
Car/driver combinations may also be subject to streakiness in consecutive races and they may also be more successful at particular venues. The empirical variables defined in the following section proxy for these effects.
Team Characteristics
Team characteristics, in particular team size, require additional explanation. It is an empirical fact that multi-car teams have, in recent years, dominated the NASCAR Winston Cup series, and it is commonly believed that multi-car teams have advantages over smaller teams. What particular advantages are possible for multi-car teams?
First, the marginal cost of increasing the speed of a car is likely to be very sharply upward sloping (Allmen, 2001). This is due in part to NASCAR rules regarding car shape, size, aerodynamics, weight, and engine characteristics. While these rules are in place to equalize competition, the existence of this degree of uniformity makes it very difficult and expensive to gain an advantage within the rules. As Bill Elliott, a driver and past owner observes, “It may cost you $5 million to get to the track, but it may cost you an additional $3 million for a few tenths better lap time ….” (Middleton, 2000, p. 37).
A team with more car/driver combinations can apply any found advantage to each of its cars. Such advantages then result in better performances for all cars on the team, and hence greater performance revenues. Consider Figure 1 in which marginal cost (MC) increases sharply as car speed increases and such costs are assumed to be the same for multi-car teams as for single car teams. Since newly discovered speed advantages can be applied to all cars on a multi-car team, those teams can generate greater revenues for the team (MR M = marginal revenue for multi-car teams) than any such advantage generates for a single car team (MR S = marginal revenue for single car teams). Following optimization principles then, multi-car teams would find it worthwhile to achieve a speed of S M, whereas single car teams have incentive to achieve a speed of only S S. If this analysis is correct, multi-car teams would be expected to achieve greater speed in general than single car teams.
Second, it is an empirical fact that larger teams attract greater sponsorship resources, in part because they are more successful. Then, if the sharply increasing marginal costs mean that multi-car teams are more likely to engage in expensive research for given performance benefits and sponsorship revenues depend on performance, the dominance of multi-car teams can be explained (at least in part) by this simple economic analysis.
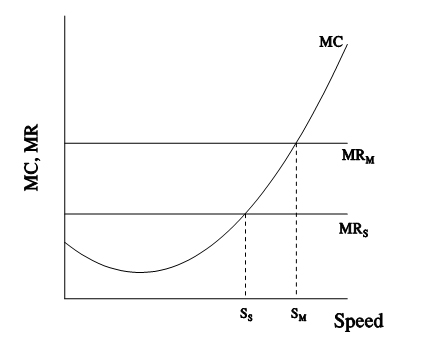
Figure 1: Multi-car versus single car teams
Third, teams with more sponsorship income are able to offer greater compensation to crewmembers, hire more experienced and specialized team members, such as aerodynamicists, and can more easily afford expensive technology and testing.
Fourth, substantial barriers to success for smaller teams (especially single car teams) may also exist because of scale economies. The advanced technology machinery for making racing parts would be an example of the “lumpy inputs” explanation of scale economies thought to be the most common reason for decreasing long run average cost. Larger teams would then have an advantage since the production of such parts for the team would necessarily be larger in scale.
Other advantages also accrue to multi-car teams. Operationally, multi-car teams also have more test dates available to them at Winston Cup tracks. Hence, more data can be collected and shared among team members when it comes to setting up the cars for races at those tracks. Multi-car teams also have built-in drafting partners, although the NASCAR literature suggests that at the end of the race each driver is “on his own,” (Cotter, 1999; Dolack, 2003; Hinton, 1997; Pearce, 1996, 2003).
Empirical Specification: Races and Data
The data for this project were collected from a variety of Web sites, http://www.nascar.com (Past Race Archive, 2002, 2003), http://jayski.thatsracin.com/ index.html (Statistics Pages from Jayski. 2002), and http://www.foxsports.com/named/ FS/Auto (Nextel Cup Standings, 2002, 2003). The variable we wish to predict is the order of finish, which is of course, available for each race on the Winston Cup circuit.
Individual Races
The 14 races for which we collected data include short tracks, speedways, super speedways, and a road course. To determine if the same factors are related to order of finish of different races at the same track, we also included both races run at Daytona and both races run at Michigan in 2003. The specific races for which we collected data are: the Brickyard 400 at Indianapolis Motor Speedway, the Food City 500 at Bristol Motor Speedway, the Coca-Cola 600 at Lowe’s Motor Speedway, the Carolina Dodge Dealers 400 at Darlington Raceway, the Daytona 500 at Daytona International Speedway, the Pepsi 400 at Daytona International Speedway, the Virginia 500 at Martinsville Speedway, the Sirius 400 at Michigan International Speedway, the GFS Marketplace 400 at Michigan International Speedway, the Chevy Rock & Roll 400 at Richmond International Speedway, the Aaron’s 499 at Talladega Superspeedway, the Samsung/Radio Shack 500 at Texas Motor Speedway, the Tropicana 400 at Chicagoland Speedway, and the Sirius at the Glen at Watkins Glen International.
The potential explanatory variables for order of finish collected for each race were as follows:
ptime = the practice time closest to race time.
qspeed = the speed at which the car/driver qualified.
pole = position of the car at the start of the race.
points = points scored in the Winston Cup Series for the prior year.
laps = number of laps completed for all Winston Cup races in the prior year.
DNF = did not finish, the number of races in which the driver failed to finish, prior year.
rookie = a dummy variable equal to 1 if the driver was a rookie in 2003, and equal to
0 otherwise.
# drivers = the number of cars/drivers a multi-car owner fields (for 2003, values = 1,2,3,4).
newteam = a dummy variable equal to 1 if the driver was a member of a new team in 2003, and equal to 0 otherwise.
prev = the finish position of the driver in the previous week’s race.
lastyr = the finish position of the driver in the 2002 running of the same race.
Car Speed
The first three variables from the above list, practice time, qualifying speed, and pole position correspond to the car speed category from the model outlined in the previous section. Clearly qualifying speed and pole position are very closely related (since pole position is determined primarily by qualifying speed), however race officials, for reasons such as a rule and/or equipment violation, missing the driver’s meeting, switching to a backup car, an engine change, or a driver change, may alter pole position. For this reason we collected data for both qualifying speed and pole position in case one or the other is a better predictor of race outcomes.
Driver Characteristics
The next four variables, points, laps, DNFs, and rookie, are driver characteristics with the first three representing performance in the prior year, and the variable rookie is a proxy for lack of experience on the Winston Cup circuit. Theoretically, rookies will not have the skill level that existing Winston Cup drivers have developed over the years, nor will they have had exposure to certain tracks that more experienced Winston Cup drivers have competed on in the past.
Team Characteristics
The variables # drivers and newteam correspond to the team characteristics category in the model. The # drivers variable measures the effect of a given owner having multiple cars/drivers or a multi-car team. With respect to the new team variable (newteam), drivers joining a new team will require time to adjust to the way the crew operates, in addition to developing an effective communication style with the crew chief.
Related Race Effects
Related race effects are measured by the variables prev and lastyr. The variable prev is an attempt to proxy for possible streakiness from race to race. That is, are good finishes followed by other good finishes and poor performances followed by poor performance in the following race? The variable lastyr attempts to measure whether a certain racetrack is a better venue for certain car/driver combinations. For example, the dominance of Dale Earnhardt, Incorporated (DEI) at the superspeedways illustrates the expertise a team may develop at specific racing venues (McCarter, 2002). Since 2001, DEI has won 9 out of the 12 races at Daytona International Speedway and Talladega Superspeedway.
Methodology and Expectations
As a first attempt to determine those variables that relate to order of finish, correlation coefficients are computed between order of finish and each of the measured explanatory variables. The following signs are anticipated for the correlation coefficients:
Expected Sign
of coefficient Explanation
![]() Faster (lower) practice time leads to better finish
Faster (lower) practice time leads to better finish
![]() Higher qualify in speed (MPH) leads to better finish
Higher qualify in speed (MPH) leads to better finish
![]() Better pole position leads to a better finish
Better pole position leads to a better finish
![]() More points from previous year leads to a better finish
More points from previous year leads to a better finish
![]() More laps completed from previous year leads to better finish
More laps completed from previous year leads to better finish
![]() More failures to finish leads to poorer finish
More failures to finish leads to poorer finish
![]() Rookies may be less likely to have better finishes
Rookies may be less likely to have better finishes
![]() Multi-car teams may have better finishes
Multi-car teams may have better finishes
![]() Driver on new teams less likely to have better finishes
Driver on new teams less likely to have better finishes
![]() Previous race finish positively related to current race finish
Previous race finish positively related to current race finish
![]() Previous finish at this track positively related to current finish
Previous finish at this track positively related to current finish
Note: ρ represents the population correlation coefficient, and f represents finish position, 1 = winner , 2 = second place, etc..
Results
Correlation Analysis
Table 1 in the appendix is the result of the correlation computations. The coefficients in bold are statistically significant at the α = .05 level and consistent with the predicted signs presented in the previous section.
Several results of this exercise are interesting and potentially important for predicting the outcome of NASCAR races. First, considering the columns (how the variables fared across different races), on average the signs of the variables are in accord with expectations (though some are on the whole insignificant). Several of the variables seem to be consistently correlated (linearly) with order of finish across races. For example the number of drivers variable (# drivers) is statistically significant for all races except Darlington and Watkins Glen (even then the coefficients have the predicted sign). Of course that teams with more members tend to be more successful is not a new conclusion—these results support statistically, at the individual race level, the hypothesis that multi-car teams are generally more successful (see the section on team characteristics above). Of the two tracks that did not have statistically significant results with respect to the # drivers variable, the Watkins Glen result might be due to the fact that it is a road race. Watkins Glen is one of only two road courses utilized by Winston Cup, and teams often use substitute drivers with more road racing skills than their full-time driver may possess in these races.
Indicators of drivers’ past successes also are correlated with order of finish. The variable points is statistically significant for 11 of the 14 races and all of these sample correlations have the anticipated sign. Interestingly enough, the three races that did not demonstrate significant results were run at Daytona and Talladega, the two restrictor plate tracks. Similarly laps, which might be interpreted as a measure of driver/car consistency and driver experience, is statistically significant in 7 of the 14 races. The DNF variable seems to explain little in the way of simple correlation with order of finish. In considering this variable, recognize that a driver with more DNFs may have simply competed in more races than another driver. Thus simple correlation, which does not control for levels of other variables, may not be appropriate to measure such effects.
Measures that account for car/driver speed include pole position (pole), qualifying speed (qspeed) and practice time (ptime). We recognize that pole position and qualifying speed generally measure the same effect. Both are included here to see if one or the other is more closely correlated with order of finish. Based on the sample correlations in Table 1, qspeed is significantly related to order of finish in half of the races and pole in 6 of the 14 races. Practice time (ptime) seems to fare somewhat better—it is significantly related to order of finish in 9 of the 14 races. There may be several reasons for this outcome. The practice times used for statistical analysis were collected from the practice session conducted closest to race time, if all drivers participated in that session. If all drivers did not participate in the last practice session, then practice time statistics were taken from the session run closest to race time in which all drivers practiced. This was done to ensure that the cars would be “set up” in practice as close to race set-up as possible. Since the cars are set-up for race conditions when they practice, it would be expected that the ptime would more closely relate to order of finish than qspeed because the set-up for qualifying is based on two laps at the fastest speed possible. Race day set-up is designed to accommodate consistency and longer runs on the track.
The variable that measures the finish position in the driver’s last race (prev) is statistically related to order of finish in 8 of the 14 races and has the expected sign for all races. This would suggest that driver/car combinations are subject to streakiness, that is, good finishes tend to be followed by other good finishes and vice versa. For only four races is the variable lastyr, the finish position of the driver in the prior running of the race by the same name correlated with the current finish position.
Of the two categorical variables, newteam (equals 1 if the driver joined a new race team for the 2003 season, 0 otherwise) is related to order of finish in 10 of the 14 races and in all races has the anticipated sign. Changing teams, on average, would seem to be related to poorer finishes. On the other hand, rookie status (rookie) was related to finish order only for the first Daytona race and Martinsville.
Again considering the columns in Table 1, the average of the correlation coefficients for each of the explanatory variables across the 14 races is included in the table as the bottom row. A coefficient above 0.25 is generally statistically significant for individual races (again α = .05, one-tailed test, n = 43) On that basis, eight of the variables (laps, points, newteam, pole, # drivers, prev, ptime, and qspeed) are on average statistically (linearly) related to order of finish.
It is also useful to consider the correlations for individual races, i.e., to consider Table 1 by row. For example, at Martinsville order of finish was linearly related to 9 of the 11 variables in the explanatory variable set. The first (June) Michigan race, Richmond, and Chicagoland were linearly related to eight of the explanatory variables. At the other end of the scale, for the two Daytona races, only two of the explanatory variables were correlated with order of finish. One of those variables was the same (# drivers) for both Daytona races. Interestingly, comparing the second (August) Michigan race to the first, only five variables were statistically significant for the second race, but each of those variables was also significant for the first Michigan race. However, relatively strong correlations for pole, practice time and qualifying speed for the first Michigan race were not repeated for the second Michigan race. The reader may examine Table 1 to see that the rest of the races have from three to seven explanatory variables that are statistically significant.
Additional Evidence on Team Effect
The effect of team membership (#drivers) seems to play an increasingly important role in NASCAR (Cotter, 1999; Dolack, 2003; Hinton, 1997; Pearce, 1996, 2003). In 2003, 12 organizations owned and fielded 33 of the 43 cars competing at the majority of NASCAR races. Additionally the Winston Cup Championship has been won by a multi-car team in each of the last 10 years (Pearce, 2003). Therefore, we considered another test of team membership on car/driver success. Using statistics from the entire 2002 and 2003 racing years, a table of results divided into top 10 finishes and finishes out of the top 10 and classified by number of team members was constructed. Table 2 in the appendix shows that teams with four members (the highest number of team members at the start of 2002) had 285 starts and of those, 43.16% resulted in top 10 finishes. The corresponding percentages are 15.55% for three member teams, 29.14% for two member teams, and only 8.68% for drivers without team members. The largest (four member) teams tended to dominate the top 10 finishes. Perhaps surprising is the fact that two member teams had by far the largest number of starts and the second highest rate of top 10 finishes with 29.14%. For three member teams the corresponding percentage was 15.55% and single drivers finished in the top 10 only 8.68% of the time. A simple chi-squared test of independence of the classification of top 10s by number of drivers on a team, yields a χ 2 = 123.9, which allows rejection of the null of independence at α < 0.001. This result confirms the obvious result that the proportion of top 10 finishes does depend on the number of team members.
Table 3 contains the same categories for the 2003 Winston Cup drivers. There was one team with five drivers for the 2003 season, so the table contains an additional column. For the 2003 season, the percentage of top 10 finishes is remarkably constant for the teams with five, four and two members, with 37%, 38% and 32% respectively. Again, teams with three members and especially the single drivers fared less well on the basis of top 10 finishes. Again, the null hypothesis of independence between number of team members and top 10 finishes can be rejected (χ 2 = 106.0), providing statistical confirmation of the already clear evidence that the proportion of top 10 finishes differs by number of team members.
Conclusions
The correlation analysis across 14 races for the 2003 NASCAR Winston Cup series identifies a number of variables that are associated with the order of finish of these races. On average, variables measuring car speed, including practice time, qualifying speed, and pole position are related to the order of finish of races. We also find that prior success on the part of the driver, measured by laps completed in the prior year and points accumulated are also correlated with order of finish. Whether or not the driver was a rookie was, perhaps surprisingly, not on average correlated with finish order across races. There is also some evidence that performances of driver/car combinations are subject to streaks. That is, finish positions in a given race are often correlated with finish positions in the race that follows. Of course these results could simply reflect the fact that some driver/car combinations consistently finish better than others may. Changing teams is correlated with poorer finishes and team size is correlated with better finishes.
The effect of team membership is reinforced by the data in Tables 2 and 3, which classifies top 10 finishes by number of team members. Teams with more members are more successful in terms of top 10 finishes. However, this effect is not monotonic in nature, since two member teams have a larger percentage of top 10s than do teams with three members.
Further research is indicated to test the robustness of these results. Such analysis could include races not in our data set and results from different years of NASCAR racing.
References
Allmen, P. von. (2001). Is the reward system in NASCAR efficient? Journal of Sports Performance, 2(1), 62-79.
Cotter, T. (1999). Say goodbye to the single-car team. Road & Track, 50(8), 142-143.
Dolack, C. (2003). One is the loneliest number. Auto Racing Digest, 31(6), 66.
Hinton, E. (1997). Strength in numbers. Sport Illustrated, 87(16), 86-87.
McCarter, M. (2002). Stepping up to the plate. The Sporting News, 226(27), 38-39.
Middleton, A. (2000, February). Racing’s biggest obstacle. Stock Car Racing, 34-37.
Past Race Archive, 2002 [Data files]. Available from NASCAR Web site, http://www.nascar.com
Past Race Archive, 2003 [Data files]. Available from NASCAR Web site, http://www.nascar.com
Nextel Cup Standings, 2002 [Data files]. Available from FOXSports Web site, http://www.foxsports.com/named/FS/Auto
Nextel Cup Standings, 2003 [Data files]. Available from FOXSports Web site, http://www.foxsports.com/named/FS/Auto
Parsons, K. (2002, August 26). Tunnel vision – NASCAR teams’ fortunes are blowing in the wind. The Commercial Appeal, Memphis, TN, p. D9.
Pearce, A. (1996). Fair and square. AutoWeek, 46(50), 40-41.
Pearce, A. (2003). Going it alone. AutoWeek, 53(14), 57-58.
Statistics Pages from Jayski. (2002) [Data files]. Available from Jayski Web site, http://jayski.thatsracin.com/index.html
Appendix
Table 1: Correlation coefficients between finish position and the explanatory variables
Explanatory Variables
| Race | Laps | DNF | Points | newteam | Pole | #drivers | prev | lastyr | ptime | qspeed | Rookie? |
| Indianapolis | -0.214 | 0.091 | -0.319 | 0.342 | -0.106 | -0.326 | 0.118 | 0.435 | 0.374 | 0.047 | 0.088 |
| Bristol | -0.209 | 0.316 | -0.350 | 0.030 | 0.177 | -0.417 | 0.117 | 0.407 | 0.392 | -0.190 | 0.088 |
| Lowe’s | -0.209 | 0.030 | -0.291 | 0.360 | 0.198 | -0.314 | 0.335 | 0.085 | 0.403 | -0.283 | 0.200 |
| Darlington | -0.373 | 0.154 | -0.428 | 0.180 | 0.176 | -0.153 | 0.170 | -0.141 | -0.239 | -0.234 | 0.265 |
| Daytona (Feb) | -0.044 | -0.111 | -0.173 | 0.155 | 0.243 | -0.300 | 0.274 | 0.045 | -0.106 | NA | 0.094 |
| Daytona (July) | -0.140 | 0.110 | -0.218 | 0.132 | 0.006 | -0.258 | 0.167 | 0.300 | 0.164 | -0.060 | 0.105 |
| Martinsville | -0.462 | 0.079 | -0.540 | 0.030 | 0.433 | -0.342 | 0.314 | 0.352 | 0.462 | -0.496 | 0.263 |
| Michigan (June) | -0.383 | 0.115 | -0.435 | 0.396 | 0.596 | -0.550 | 0.478 | 0.125 | 0.549 | -0.547 | 0.041 |
| Michigan (Aug) | -0.342 | -0.297 | -0.408 | 0.380 | 0.172 | -0.356 | 0.392 | 0.087 | 0.237 | -0.205 | 0.212 |
| Richmond | -0.367 | -0.070 | -0.508 | 0.384 | 0.406 | -0.283 | 0.300 | 0.126 | 0.350 | -0.403 | 0.228 |
| Talladega | -0.228 | 0.088 | -0.230 | 0.306 | 0.398 | -0.335 | 0.098 | 0.233 | 0.080 | -0.361 | 0.170 |
| Texas | -0.200 | 0.085 | -0.352 | 0.282 | 0.169 | -0.393 | 0.195 | -0.178 | 0.300 | -0.159 | 0.146 |
| Chicagoland | -0.339 | 0.064 | -0.413 | 0.260 | 0.422 | -0.261 | 0.317 | 0.246 | 0.428 | -0.464 | 0.178 |
| Watkins Glen | -0.410 | -0.298 | -0.472 | 0.406 | 0.297 | -0.244 | 0.254 | 0.123 | 0.285 | -0.278 | 0.239 |
| Average | -0.280 | 0.025 | -0.367 | 0.260 | 0.256 | -0.324 | 0.252 | 0.160 | 0.263 | -0.279 | 0.166 |
Table 2: Top Ten Finishes by Number of Team Members, 2002 Season
| 4 member teams | 3 member teams | 2 member teams | One member teams | |
| Top 10 % | 43.16% | 15.55% | 29.14% | 8.68% |
| Total starts | 285 | 328 | 525 | 357 |
Table 3: Top Ten Finishes by Number of Team Members, 2003 Season
| 5 member teams | 4 member teams | 3 member teams | 2 member teams | One member teams | |
| Top 10 % | 36.87% | 38.19% | 22.53% | 31.67% | 7.66% |
| Total starts | 179 | 144 | 395 | 360 | 418 |
The flat MR curves are offered as an approximation. Additional speed should add increasing marginal revenue (as cars move up in finish order, added revenue increases), but since all cars are attempting to increase speed, the possible increases in revenue will be distributed among the competitors.
For example, testing for the aerodynamic properties of a car in a wind tunnel can cost more than $2000 per hour (Parsons, 2002).
T he field is generally set using a combination of timed laps and provisionals. The fastest 36 cars earn a place based on time, while positions 37-43 are determined by a process which may include last season’s final owners standings, current owners standings and former champions. The provisionals are assigned in descending order, beginning with the highest ranking owner in the standings. The lone exception is the Daytona 500, which uses two qualifying races to determine the field. (Nascar.com)
In other words, a driver with many laps completed and many DNFs would be expected to fare less well than another driver with many laps completed, but few DNFs.
While the sample size is generally 43 for individual races it is somewhat lower for some individual races, e.g., a race in which a driver/car combination did not run in the race at a particular venue it its previous iteration.
If all four members of a team start in the same race, that would equal 4 starts and if two of those four finish in the top 10, that would be 50% in the top 10.
This procedure can also be described as a test of proportions, that is, we have evidence that the proportions of top 10 finishes differs by number of team members.
