Authors: Jason C. Casey1, Robert L. Herron2, and Michael R. Esco3
1Department
of Kinesiology, University of North Georgia, Oakwood, GA, USA
2Department of Sports Management, United States Sports Academy,
Daphne, AL, USA
3Department of Kinesiology, The University of Alabama, Tuscaloosa,
AL, USA
Corresponding Author:
Robert L. Herron, MA, CSCS*D, ACSM-RCEP
1 Academy Drive
Daphne Al, 36526
rherron@ussa.edu
251-626-3303
Jason C. Casey, PhD, CSCS*D, EP-C is an Assistant Professor of Kinesiology at the University of North Georgia in Oakwood, GA. His research interests focus on fatigue and recovery associated with exercise, athlete monitoring, and sport-related measurement issues.
Robert L. Herron, MA, CSCS*D, ACSM-RECP is currently faculty member and Sport Management doctoral student at the United States Sports Academy. Robert’s areas of research interest include: measurement and evaluation in sport-related research and recovery from exercise stressors or sport injuries.
Michael R. Esco, PhD, CSCS*D, FACSM is an associate professor of exercise physiology in the Department of Kinesiology at the University of Alabama. His research interests are in the areas of heart rate variability, body composition, athletic monitoring, and cardiovascular physiology.
Comparison of BMI-based equations and plethysmography for estimating body fat in female collegiate gymnasts
ABSTRACT
The purpose of this study was to assess the utility of using BMI-based equations (BEQ) to estimate body-fat percentage (BF%) in female-collegiate gymnasts. As such, the agreement between BF% estimates with BEQ and air-displacement plethysmography (AP) were compared in twenty-two gymnasts (n = 22). Body mass, height, and BF% were assessed via AP and BEQ [Jackson et al. (JBMI), Deurenberg et al. (DBMI), and Womersley & Durnin (WBMI)]. Results: The assessments produced the following estimated BF%: AP = 20.3 ± 3.6%; JBMI = 26.9 ± 3.9%; DBMI = 26.4 ± 2.2%; and WBMI = 27.9 ± 2.5%. BF% estimated via AP was significantly lower (p < 0.001) than each BEQ. Weak correlations were found between AP and BEQ (JBMI, r = 0.12; DBMI, r = 0.07; WBMI, r = 0.12). The limits of agreement (constant error ± 1.96 SD) for each BEQ compared to AP were: JBMI = 6.6 ± 9.5%; DBMI = 6.1 ± 7.8%; and WBMI = 7.6 ± 8.0%. These results suggest a wide range of individual differences existed between BEQ and AP. Furthermore, BEQ significantly overestimated BF% relative to AP in this gymnastics population. Coaches and sport practitioners are in need of a quick, practical, inexpensive, and accurate method of body composition assessment. Based on this study, BEQ does not meet the needs of the practitioner when compared to AP. As a result, practitioners in the field need to consider other field methods of predicting BF% in collegiate female gymnasts.
Keywords: air-displacement, body mass index, percent fat, gymnastics
INTRODUCTION
Many factors, including body composition, influence performance and health of athletes. Desirable ranges of body fat percentage (BF%) and other anthropometric measurements vary between athletes, sports, and positions (9, 20). However, it is generally considered that increased fat-free mass (FFM) is beneficial and excess fat-mass (FM) is a detriment to athletic performance (11).
Coaches and other sport practitioners need a body-composition assessment method to be valid, accessible, and easy to use (1). Body mass index (BMI) is one of the most commonly utilized body composition metrics and a popular method used to determine the body size clasifications in the general population (24). BMI assessment is non-invasive and requires only a measurement of height and weight. Thus, BMI is quite easy to assess, does not require a skilled technician, and is a time-efficient method of body composition analysis. A primary concern of BMI is that the metric fails to distinguish between fat mass and fat-free mass and BMI alone may misclassify obesity in some populations (14). Despite these limitation, research has shown that BMI and BF% are highly correlated in the general population (18). To better utilize this metric, several regression equations have been developed to estimate BF% with BMI as a primary variable (6, 13, 26). However, little research has been conducted evaluating these equations in an athletic population.
Valid laboratory methods of assessment have been used to estimate BF% and other body-composition metrics in athletes – such as underwater weighing and dual-energy x-ray absorptiometry (10, 15). However, these methods are often expensive, difficult to access and require a highly trained technician. Additionally, research has demonstrated value of various field techniques which are often popular in a practical setting due to the accessibility and ease of use (8, 15). Nevertheless, these techniques present different challenges. For instance, small changes in hydration status and fluid balance can influence the accuracy of BIA assessment. Thus, controlling for hydration should be a requirement with BIA but often ignored in practical settings (8, 17). Skinfold assessment has been shown to be accurate relative to laboratory methods (15). However, skinfold assessment requires a skilled technician that is trained to precisely locate anatomical markers and measure skinfold thickness at specific locations on the body (3). Furthermore, there are and over 100 various body composition equations that may contribute to validity and reliability issues (3). An alternative laboratory-based body composition assessment method is air-displacement plethsymography (AP). AP is often deemed a faster and more user-friendly laboratory measure (23) and is regularly used in athletic settings. Additionally, evidence supports the use of AP as a valid estimate of BF% in female athletes when compared to dual energy x-ray absorptiometry (DXA) (1). Furthermore, AP has recently been used in the establishment of descriptive values for body composition across a large sample of female-collegiate athletes (9).
In women, excessively low BF% is linked with the deleterious health conditions comprising the female athlete triad including; disordered eating, low bone mineral density, and amenorrhea (7, 20). Additionally, extreme weight loss and the related comorbidities are more common in sports where aesthetics is a prominent aspect of the culture. As noted in previous research, some female gymnasts, attempting to aesthetically conform for sport, are known to achieve these physical goals by engaging in extreme weight loss behaviors associated with disordered eating (12, 22).
Furthermore, in sports where aesthetics are a prominent aspect of the associated culture, such as gymnastics (20), researchers have documented that, in female athletes, appearance is a major factor influencing body composition (19). Moreover, one’s sense of body image may be distorted in female athletes participating in these sports (5, 25), even among athletes who present with a favorable body composition (5). As a result, the importance of regular, accurate assessment of BF% are heightened in these female athletes and – more importantly – inaccurate estimates of BF% may detrimentally impact the physical and psychological well-being of the athlete.
Due to their speed and simplicity, BEQ may be attractive for coaches and sport practitioners who have limited access to more advanced measures (such as AP), have minimal time for body composition assessment, or have limited training in techniques like skinfold assessment. However, there is little research available to compare BF% estimations from BEQ versus more advanced methods in athletes. The purpose of this study was to assess the utility of using BMI-based equations (BEQ) to estimate body-fat percentage (BF%) in female-collegiate gymnasts.
METHODS
Participants
This study utilized data from twenty-two (n = 22) female collegiate gymnasts (age = 19 ± 1 yr, height = 158.2 ± 1.9 cm, body mass = 57.4 ± 5.6 kg, and BMI = 22.9 ± 1.8 kg.m-2). This study was approved by the Institutional Review Board at The University of Alabama.
Procedures
To compare three previously developed BEQ with AP, data was analysed from a de-identified database. Information obtained from this database for the purposes of this study consisted of height, body mass, body composition via AP, and age. BMI was then calculated and subsequently, BF% estimates were derived from the BEQ (6, 13, 26). BF% estimates from each BEQ were then compared to BF% estimates determined via AP.
Participants were instructed to refrain from exercise, eating, and drinking for at least 2 hours before testing. Height was measured to the nearest 0.1 cm using a stadiometer (Detecto, Webb City, MO) and body mass was measured to the nearest 0.02 kg via the BOD POD electronic scale, calibrated to manufacturer guidelines with participants’ bare foot. BMI was calculated as mass (kg) divided by height (m2). All values for BMI were rounded to the nearest 0.1 kg.m-2.
Body composition was assessed via AP using a calibrated BOD POD (BOD POD body-composition system, model 2000A; Life Measurement Instruments, Concord, CA). Prior to each testing session, all BOD POD calibration procedures were completed according to the manufacturer guidelines by measuring an empty chamber and a calibrating cylinder of a standard volume (49.55 L). Researchers proceeded after successful calibration. Participants wore a tight-fitting spandex sports bra, spandex shorts, removed all jewelry, and were provided a swim cap to wear over their head to minimize the effect of hair on body volume assessment. A trained technician then performed the BOD POD assessment.
Participants were asked to sit in the BOD POD in an erect position with hands folded in their laps for body volume assessment. All BOD POD instructions were followed for the assessments. As directed by the manufacturer, two tests were performed to ensure reliability of the assessment. If the two original tests were not within 150 mL of each other, two additional tests were performed to achieve reliable data. This method of assessment is recommended by the manufacturer. Previous literature has demonstrated high test to test reliability of AP via these methods for body mass (r = 1.0), BF% (r = 0.997), and fat-free mass (FFM) (r = 1.0) (9).
After completion of the test, the software predicted the following in all participants: thoracic gas volume, fat-free mass (FFM), fat mass (FM), and BF%. BF% was also predicted via the following three previously developed BEQ: Jackson et al. (JBMI) (13), Deurenberg et al. (DBMI) (6), and Womersley & Durnin (WBMI) (26). See Table 1 for the equations.
Table 1. BMI-based BF% regression equations that were utilized within the study.| Abbreviation | Equation |
| JBMI | (4.35 x BMI) – (0.05 x BMI2) – 46.24 |
| DBMI | (1.20 x BMI) + (0.23 x age) – 5.4 |
| WBMI | (1.37 x BMI) – 3.47 |
Data Analyses
Statistical analyses were performed using SPSS version 20.0 (IBM, Somers, NY, USA). A repeated-measures analysis of variance (ANOVA) was performed to determine mean differences between BF% assessed via AP and the three BEQ using an alpha level of 0.05. A Bonferonni post-hoc analysis was used as a follow-up procedure for pair-wise comparisons. Pearson product-moment correlation coefficients, Cohen’s d effect size (4), constant error, and the 95% limits of agreement via the Bland-Altman method (2) were also calculated.
RESULTS
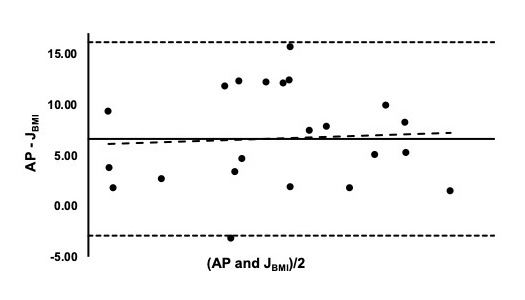
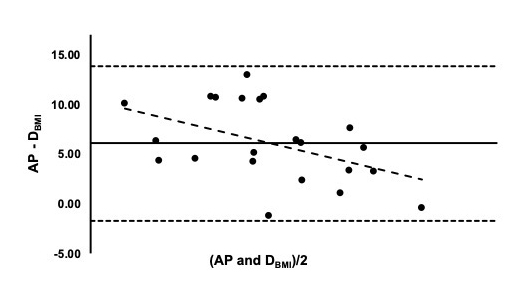
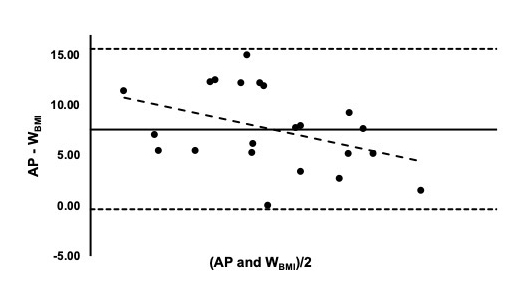
Table 2 represents the comparative statistics between AP and the BEQ. As indicated by the repeated measures ANOVA and follow-up post hoc analysis, each BEQ provided a significantly higher estimation of BF% when compared to AP (p < 0.001). WBMI estimated the highest BF% and was statistically higher than JBMI (p = 0.03) and DBMI (p < 0.001). Furthermore, the effect size for the comparison of AP to each BEQ was classified as large (Cohen’s d > 0.8). Weak correlations were found between AP and all BEQ. Additionally, AP had a weak correlation with BMI (r = 0.17).
Table 2. BMI-based equations compared to AP (n = 22) (mean ± SD).| Method | Body Fat % | Cohen’s d | r | CE ± 1.96 SD |
| AP | 20.3 ± 3.6 | – | – | – |
| JBMI | 26.9 ± 3.9* | 0.9 | 0.12 | 6.6 ± 9.5% |
| DBMI | 26.4 ± 2.2* | 1.0 | 0.07 | 6.1 ± 7.8% |
| WBMI | 27.9 ± 2.5* | 1.2 | 0.12 | 7.6 ± 8.0% |
| Cohen’s d = effect size compared to with AP r = Pearson product-moment correlation coefficient with AP. *Significantly greater than AP, (p < 0.001). |
||||
Bland-Altman plots evaluating the individual differences between AP and each BEQ are shown in Figures 1-3. The mean bias predicted for JBMI was 6.6% and the ± 1.96 SD ranged from -2.9% to 16.1% (Figure 1). As seen in Figure 2, the mean bias for DBMI was 6.1% ranging from (± 1.96 SD) -1.7% to 13.9%. The mean bias for WBMI was the largest at 7.6% and the ± 1.96 SD ranged from -0.4% to 15.6% (Figure 3).
DISCUSSION
The purpose of this study was to determine the agreement between three BEQ and AP for estimating BF% in female collegiate gymnasts. BEQ provide quick and simple methods of estimating BF% that, if in agreement with more advanced assessment methods, would allow for increased accessibility and ease of testing for practitioners in athletic settings. However, this study found that each BEQ provided a significantly higher estimate of BF% than AP. Additionally, all BEQ showed a wide range of individual error relative to AP (each BEQ demonstrated a constant error of > 6.0%) according to the Bland-Altman method, as well as weak correlation coefficients. Furthermore, AP had a weak correlation with BMI alone (r = 0.17). Thus, it is recommended that practitioners avoid the use of BEQ in the female collegiate gymnast population.
Gymnasts typically maintain a lower BF% and greater FFM (considered an athletic body type) compared to the average population. This likely serves as an explanation for the results found in this study, as BMI does not distinguish between FM and FFM often misclassifying individuals with athletic body types (16). Thus as the results of this study indicate, the equations predominately dependent on BMI were not able to accurately predict BF% relative to AP in this sample of collegiate female gymnasts. It should be noted that it may be advantageous for the gymnastics athlete at this level of competition to have a lower body height. Fields et al. (2017) demonstrated that body height for female collegiate gymnasts was statistically lower than five other collegiate female sports evaluated (9). Due to this typical body type (lower BF%, increased FFM, and lower body height) BMI-based categorical interpretation, serves little-to-no use in the collegiate, female-gymnast population.
There were limitations to this study that may have impacted the results. Three specific limitations were: hydration status was not measured in the participants, phase of the menstrual cycle was not taken into consideration, and residual volume was estimated via AP standard process as opposed to directly measuring. Each of these could have impacted body composition measurement. However, because all measurements were performed during one session, the influence of total body water status would have influenced body weight for all measures, making the impact on the results minimmal.
Further research to provide sport practioners with a quick and accurate method of assessing BF% should focus on formulas with additional variables that do not rely as heavily on BMI. Taylor et al. (2012) developed a formuala utilizing BMI, hand-grip strength, waist circumference, and sex as variables (21). The results of the study indicated the BF% estimation from the formula did not differ from dual-energy x-ray absoptiomitry (DXA). In additon, the formula had a high correlation and low standard error of the estimate relative to DXA. However, this study included only participants from the general population. It is unknown if the inclusion of these additional variables in the BF% estimation formula would result in a more accurate estimate of BF% in female athletes – more specifically – female gymnasts.
CONCLUSIONS
Regular monitoring of body composition is a valuable component of strength and conditioning programs. Coaches and sport practitioners are in need of a quick, practical, inexpensive, and valid method of body composition assessment. BEQ significantly overestimated BF% relative to AP in this gymnastics population. This indicates that the BEQ did not appropriately estimate group-mean BF%. Furthermore, a wide range of individual differences existed when comparing the three BEQ with AP estimates in female-collegiate gymnasts.
APPLICATIONS IN SPORT
Due to the aesthetic focus of gymnastics, inaccurate body composition data can foster unhealthy body-image perceptions and exacerbate psychological issues related to the development and progression of eating disorders (5, 20). Therefore, coaches and other sport practitioners should refrain from using BEQ in female-collegiate gymnasts and should consider other practical means of predicting BF% in this population.
REFERENCES
- Ballard TP, Fafara L, and Vukovich MD. Comparison of BOD POD and DXA in female collegiate athletes. Medicine & Science in Sports & Exercise 36: 731-735, 2004.2. Bland JM and Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet (London, England) 1: 307-310, 1986.
- Bland JM and Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet (London, England) 1: 307-310, 1986.
- Campbell BI and Spano MA. NSCA’s guide to sport and exercise nutrition. Champaign, IL : Human Kinetics, ©2011., 2011.
- Cohen J. Statistical power analysis for the behavioral sciences. 1988.
- de Oliveira GL, de Oliveira TAP, de Pinho Gonçalves PS, Valentim Silva JR, Roquetti Fernandes P, and Fernandes Filho J. Body image and eating disorders in female athletes of different sports. Journal of Exercise Physiology Online 20: 44-54, 2017.
- Deurenberg P, Weststrate JA, and Seidell JC. Body mass index as a measure of body fatness: age- and sex-specific prediction formulas. The British journal of nutrition 65: 105-114, 1991.
- Donaldson ML. The female athlete triad. A growing health concern. Orthop Nurs 22: 322-324, 2003.
- Esco MR, Olson MS, Williford HN, Lizana SN, and Russell AR. The accuracy of hand-to-hand bioelectrical impedance analysis in predicting body composition in college-age female athletes. National Strength and Conditioning Association, 2011, p 1040.
- Fields JB, Metoyer CJ, Casey JC, Esco MR, Jagim AR, and Jones MT. Comparison of Body Composition Variables Across a Large Sample of National Collegiate Athletic Association Women Athletes From 6 Competitive Sports. J Strength Cond Res 32: 2452-2457, 2018.
- Fleck SJ. Body composition of elite American athletes. The American Journal of Sports Medicine 11: 398-403, 1983.
- Garrett WE and Kirkendall DT. Exercise and sport science. Philadelphia: Lippincott Williams & Wilkins, 2000.
- Harris MB and Greco D. Weight control and weight concern in competitive female gymnasts. Journal of Sport & Exercise Psychology 12: 427-433, 1990.
- Jackson AS, Stanforth PR, Gagnon J, Rankinen T, Leon AS, Rao DC, Skinner JS, Bouchard C, and Wilmore JH. The effect of sex, age and race on estimating percentage body fat from body mass index: The Heritage Family Study. International Journal Of Obesity And Related Metabolic Disorders: Journal Of The International Association For The Study Of Obesity 26: 789-796, 2002.
- Jitnarin N, Poston WSC, Haddock CK, Jahnke SA, and Day RS. Accuracy of Body Mass Index-defined Obesity Status in US Firefighters. Safety and health at work 5: 161-164, 2014.
- Moon JR, Tobkin SE, Smith AE, Lockwood CM, Walter AA, Cramer JT, Beck TW, and Stout JR. Anthropometric estimations of percent body fat in NCAA Division I female athletes: a 4-compartment model validation. J Strength Cond Res 23: 1068-1076, 2009.
- Nevill AM, Stewart AD, Olds T, and Holder R. Relationship between adiposity and body size reveals limitations of BMI. American Journal of Physical Anthropology 129: 151-156, 2006.
- Saunders MJ, Blevins JE, and Broeder CE. Effects of hydration changes on bioelectrical impedance in endurance trained individuals. Med Sci Sports Exerc 30: 885-892, 1998.
- Sun Q, van Dam RM, Spiegelman D, Heymsfield SB, Willett WC, and Hu FB. Comparison of Dual-Energy X-Ray Absorptiometric and anthropometric measures of adiposity in relation to adiposity-related biologic factors. American Journal of Epidemiology 172: 1442-1454, 2010.
- Sundgot-Borgen J. Risk and trigger factors for the development of eating disorders in female elite athletes. . Medicine & Science in Sports & Exercise 26: 414-419, 1994.
- Sundgot-Borgen J and Garthe I. Elite athletes in aesthetic and Olympic weight-class sports and the challenge of body weight and body compositions. J Sports Sci 29: S101-114, 2011.
- Taylor JK, Esco MR, Williford HN, McHugh AN, Bloomquist BE, and Mahurin AJ. Handgrip Strength Enhances the Utility of Traditional Body Composition Parameters with Predicting Percent Body Fat. Medicine and science in sports and exercise 44: 801, 2012.
- Thompson A, Petrie T, and Anderson C. Eating disorders and weight control behaviors change over a collegiate sport season. Journal of Science & Medicine in Sport 20: 808-813, 2017.
- Wagner DR and Heyward VH. Techniques of body composition assessment: A review of laboratory and field methods. Research quarterly for exercise and sport 70: 135-149, 1999.
- WHO. Physical status: the use and interpretation of anthropometry. Report of a WHO Expert Committee. World Health Organization technical report series 854: 1-452, 1995.
- Wilmerding MV, McKinnon MM, and Mermier C. Body composition in dancers: a review. Journal of Dance Medicine & Science 9: 18-23, 2005.
- Womersley J. A comparison of the skinfold method with extent of ‘overweight’ and various weight-height relationships in the assessment of obesity. The British journal of nutrition 38: 271-284, 1977.

