A New Method for Ranking Total Driving Performance on the PGA Tour
Abstract
The Professional Golf Association Tour (PGA Tour) currently ranks its players according to their overall Total Driving performance by adding together individual ranks for their average driving distance and for their driving accuracy percentage. However, this widely used and reported measure is inappropriate because it is based upon the addition of two ordinal-scaled measures in which the underlying differences between successive ranks are not equal. In this paper, we propose a new method for ranking golfers in terms of their overall driving performance. The method eliminates the drawbacks of previously reported measures, including the one used by the PGA Tour. Using the new methodology, we re-rank all PGA Tour golfers for the 2005 season and compare these ranks to the “official” ranks reported by the PGA Tour. In some cases, large differences in players’ rankings existed. The reasons for these differences are then discussed.
Introduction
In recent years, numerous statistical analyses have been conducted in an attempt to assess the relative importance of various shot-making skills on overall performance on the PGA Tour and among amateur golfers (Shmanske, 2000; Dorsel and Rotunda, 2001; Engelhardt, 1997 and 2002; Callan and Thomas, 2004 and 2006; and Wiseman and Chatterjee, 2006). While most of the measures that have been used in these analyses have been well-defined and widely accepted, there is one performance statistic, “Total Driving,” that has not been well-defined. This particular statistic, which combines a golfer’s (i) average driving distance and his/her (ii) driving accuracy percentage, has been operationally defined in numerous ways, but no methodologically sound measure has emerged to date. This includes the measure now being used by the PGA Tour.
In this paper, the authors propose a new statistical measure based upon standardized z-scores for ranking golfers according to Total Driving performance. This new measure eliminates the methodological drawbacks of previously developed measures by re-ranking PGA Tour golfers on their Total Driving performance during the 2005 season and comparing these rankings to the “official” PGA Tour rankings for that season.
The evolving nature of the relationship that has existed between driving distance and driving accuracy on the PGA Tour over the last sixteen years (1990-2005) was examined. Then, alternative ranking methods that have been proposed and the necessity of and the rationale for a new composite measure of Total Driving performance were discussed. Following this, the new measure can be applied to the 2005 PGA Tour season. These new rankings dramatically alter the previous ranking of many golfers on the tour. The reasons for the differences in rankings will be explored.
Distance and Accuracy on the PGA Tour: 1990-2005
The average driving distances and the driving accuracy percentages have changed significantly since 1990, with the largest changes taking place in recent years. This is shown in Table 1. The average driving distances have increased every year since 1993 and these increases have been relatively steady on a year-by-year basis, except in 2001 and 2003, when the increases were significantly higher. We surmise that technological improvements in golf balls and equipment are likely to have played a part in these two years.
A similar trend did not exist for the driving accuracy percentage. Here, the accuracy percentage steadily increased from 1990 to 1995, and then remained relatively stable over the next six-year period, only to decline dramatically in the last few years. This dramatic decline occurred at the same time that the average driving distance substantially increased. In fact, during the 2005 PGA Tour season, the average driving distance was at its sixteen year high of 288.6 yards and the driving accuracy percentage was at its sixteen year low at 62.8%.
The negative relationship between a golfer’s average driving distance and driving accuracy percentage increased in strength over this sixteen year period. As indicated in Table 1, the strength of the relationship has grown in recent years and it reached its highest level in 2005, when the correlation between the two measures was -.679.
Current Measures of Total Driving Performance
Ranking golfers on each of the two driving measures presents no problems. Driving distance is simply defined as the average number of yards per measured drive. For each golfer, these drives are measured on two holes per round. Driving accuracy is the percentage of all drives that come to rest in the fairway. However, the PGA Tour and others (for example, Engelhardt, 1997) have indicated the need for a single measure that takes into account both the driving accuracy percentage and the average driving distance. Numerous researchers have attempted to obtain such a measure; unfortunately all of the measures that have been proposed have had methodological flaws associated with them.
The most widely used measure is the one used by the PGA Tour. It is obtained by adding together the individual ranks of a golfer on each of the two measures and then obtaining a final overall ranking based upon the total score. That is, for example, a golfer who was ranked 32nd in driving distance and 42nd in driving accuracy percentage would have a total score of 32+42=74. The PGA Tour would rank such a golfer higher than another golfer who ranked, for example, 25th in average driving distance and 60th in driving accuracy percentage, since the former summated score of 74 is lower than the latter summated score of 85.
Such an approach is flawed despite its widespread use and acceptance. The major flaw is that the level of measurement of each of these two rankings (driving distance and driving accuracy) is at the ordinal level and, as such, it does not take into account the underlying differences in distances or in driving accuracy percentages. Stated differently, while the differences in successive ranks remain the same, the corresponding differences in distance and accuracy are not equal. Thus, it is not possible to add the distance and accuracy ranks directly, without loss or distortion of the underlying information.
Davidson and Templin (1986) suggested a somewhat different approach. They proposed a measure which first divided all PGA Tour players into three groups based upon their average driving distance. They then made a similar classification based upon the driving accuracy percentage. The three groups were coded as 1 (top one-third), 2 (middle one-third), and 3 (bottom one-third). To arrive at a measure of Total Driving performance, the researchers multiplied the individual coded scores of each golfer. The larger the score, which ranged from 1 to 9, the better the performance. The authors used this new measure in a multiple regression analysis in an attempt to isolate the effects of driving on overall scoring performance.
This measure was questioned by Belkin et al. (1994) because no evidence was provided to support the construct validity of the measure and because of the multiplication of the individual codes at the ordinal level of measurement.
More recently, Wiseman and Chatterjee (2006) proposed a multiplicative measure of Total Driving which ranked golfers according to the product of their average driving distances and their driving accuracy percentages. Essentially, this measure reduced golfers’ average driving distances by the proportion of times their drives did not land on the fairway. Thus, a golfer who had an average driving distance of 300 yards and an accuracy percentage of 60% would be ranked lower than another golfer who had an average driving distance of 280 yards and an accuracy percentage of 70%, since 300(.60) =180 < 280(.70)=196. This measure was found to be highly correlated with the PGA Tour measure, but subsequent analyses revealed that it was also flawed because it gave far greater weight to driving accuracy than it did to driving distance. However, unlike the two previously discussed measures, it was operationally sound in that it was appropriate to multiply the two quantities together.
In summary, different measures for Total Driving performance that have been used are all flawed, and it is difficult to justify any of them as an appropriate measure. In the next section of this paper, a new method for ranking golfers that have none of the drawbacks of the previously discussed measures will be explained.
A New Measure for Ranking Total Driving Performance
Both average driving distance and the driving accuracy percentage are ratio-scaled data. To combine these two measures into a single overall measure of Total Driving performance, the measure we propose is based upon two statistically independent standardized z-scores, one for driving distance, and the other for driving accuracy given driving distance.
In proposing such a measure, if the distance and accuracy measures are statistically independent and they are viewed as being of equal importance in driving performance, then it would be reasonable to compute the standardized z-score of each measure, and then to add these z-scores to arrive at an overall score. However, this approach does not seem reasonable in the present situation because (i) there is a strong negative correlation between driving distance and driving accuracy, and (ii) driving distance is the primary factor in determining accuracy, rather than the other way around (driving distance is primarily a function of a player’s physical strength and athletic ability). With this reasoning, we propose the following as a composite score of Total Driving:
Zsum = ZDD + ZDA|DD
where:
ZDD = Standardized z-score of
driving distance, and
ZDA|DD = Standardized z-score
of driving accuracy given driving distance.
To compute ZDD for a player, we subtract the average driving distance for all players, µDD, from the given player’s average driving distance, DD, and divide the result by the standard deviation of average driving distances, σDD. This is expressed as:
| ZDD= | DD-µDD |
| σDA|DD |
Computation of ZDA|DD is a somewhat more involved procedure. We need to determine the mean or expected accuracy percentage of all golfers who drove the ball a specified average distance, DD, as well as the standard deviation of the driving accuracy percentages given the specified average distance, DD. The formulas for these are:
µDA|DD = ρσDA((DD-µDD)/σDD),
and σDA|DD = √((1-ρ2)σDA2
where ρ is the correlation coefficient between distance and accuracy.
The conditional standardized z-score of driving accuracy given driving
distance is then computed using the following formula:
ZDA|DD = (DA – µDA|DD) / √((1-ρ2)σDA2.
Statistical theory about bivariate normal distributions tells us that z-scores for distance and accuracy, ZDD and ZDA|DD, both have a mean of 0.0 and a standard deviation of 1.0. Further, the conditional z-score for accuracy given distance, ZDA|DD, is statistically independent of the z-score for driving distance, ZDD.
Because the two standardized z-score measures are statistically independent, and because ZDA|DD is an indicator of accuracy after taking distance into account, they can be added together to obtain an overall summated z-score for overall driving performance. The higher the overall value of Zsum = ZDD + ZDA|DD, the better the overall performance.
The authors will discuss in greater detail the application of this approach for ranking golfers based upon their Total Driving performance in the 2005 PGA Tour season.
Application to the 2005 PGA Tour Season
In 2005, there were 202 golfers on the PGA Tour. Detailed statistical data for these players can be found on the PGA Tour’s website (www.pgatour.com). Anderson Darling’s (AD) test was used to determine if driving distance has a normal distribution. With this test, we reject the null hypothesis that the data came from a normal distribution if the AD statistic is very large, or equivalently, if the p-value is smaller than a chosen level of significance (usually 0.05 or 5% level of significance). Our data show that the AD statistic was 0.367, which is small, and the p-value is 0.429, which is larger than the 5% level of significance. Therefore, we do not reject the hypothesis that the data came from a normal distribution.
Similarly, we used the AD statistic to test whether the driving accuracy percentage variable was Normally distributed. The AD test produced a test statistic of 0.350 with a p-value of 0.471. As a result, we do not reject the hypothesis that the driving accuracy percentages are Normally distributed. Given these results, we concluded that the joint distribution of driving accuracy and driving distance can be represented by a bivariate Normal distribution, with a correlation coefficient of ρ = -.679 between the two variables.
Next, the authors computed the values of Zsum as the Total Driving scores, and ranked these values in descending order. The scores for the top forty players in the resulting ordering, together with the corresponding PGA Tour ranks, are shown in Table 2.
As it is seen in Table 2, Tiger Woods was the number one ranked golfer in terms of Total Driving under the proposed method, which stands in sharp contrast to his rank of 83rd in the PGA Tour rankings. In terms of average driving distance, Woods was ranked 2nd in 2005 among 202 Tour players with an average driving distance of DD = 316.1 yards. The top ranked player was Scott Hend, who had an average driving distance of 318.9 yards. Woods’ average driving accuracy percentage of DA = 54.6% gave him a PGA Tour ranking of 188th on this measure. The top ranked player was Jeff Hart with a driving accuracy percentage of 76.0%. Woods’ two ranks of 2nd and 188th led to his overall ranking of 83rd for Total Driving based upon the PGA Tour method.
To illustrate the computation of ZDD , ZDA|DD , and Zsum for Tiger Woods, in 2005, the average driving distance among all players was 288.6 yards with a standard deviation of 9.32 yards. The average for the driving accuracy percentage was 62.8% with a standard deviation of 5.32%. As noted previously, the correlation between driving accuracy and driving distance was -.679. Then, the standardized driving distance z-score for Tiger Woods is:
ZDD = (316.1 – 288.6) / 9.32 = 2.95.
The conditional mean driving accuracy percentage given the average driving distance of 316.1 yards is:
µDA|DD = 62.8% + (-.679)(5.32%)(2.95)
= 52.1%.
That is, Tiger Woods or any golfer who has an average driving distance of 316.1 yards would be expected to have a driving accuracy percentage of 52.1%. Since Woods’ actual driving accuracy percentage for 2005 was 54.6%, his conditional z-score would be equal to:
ZDA|DD = (54.6 – 52.1) / √((1-(-.679)2)(5.32)2)
= .63
By adding the two z-scores for Tiger Woods, an overall Zsum score of 3.58 is obtained, which is the highest of any of the PGA Tour
players in 2005.
The rationale for Woods’ jump in the rankings can be seen by a closer examination of the z-scores. His average driving distance of 316.2 yards far outdistanced all other golfers (except one). His z-score value of 2.95 reflects this large differentiation, whereas previously his ranking of 2nd did not because it assumed that the distances between ranks were equal when they were not. Further, his conditional z-score for driving accuracy is now positive where before it was negative. The reason for this is because his relatively low driving accuracy percentage of 54.6% did not reflect at all how far Woods drove the ball. Actually, for those who drive the ball this far, a driving accuracy percentage approximately two percentage points lower could be expected. These two factors taken together accounted for his top ranking.
The Spearman rank correlation between the PGA Tour rankings and the new rankings was computed to be rs = .90 (p < .001). This shows that there was a large degree of similarity between the two rankings. On the other hand, and as illustrated by the case of Tiger Woods, there were also dramatic differences in some cases. To get a better feel for the differences, consider the scatterplot of the rankings under the two methods, which is shown in Figure 1. It is seen that the rankings under the two methods are generally similar, particularly in the middle range of rankings, but discernibly less so near the top or the bottom ranges. Divergence of the rankings at the extremes in this way emphasizes the effect of the ranking method on the results, which in turn brings the virtues and flaws of the ranking methods into focus.
Golfers whose rank improved included V. J. Singh, from 38th to 13th, Davis Love III, from 59th to 11th, and Brett Wetterich, from 73rd to 4th. Those going in the opposite direction included Marc Calcavecchia, from 21st to 45th, Jonathan Kaye, from 23rd to 44th, and Justin Rose, from 13th to 33rd. Typically, the reason for a golfer improving rank is because one of the measures was quite good and the standardized z-scores now reflect this, while the previous ranking system did not. For those golfers falling in rank, their old ranks tended to be clustered around many other golfers and their actual differences in rank did not reflect this closeness. For example, Justin Rose had a driving accuracy percentage of 63.7%, which gave him a ranking of 81st among all golfers on this measure. However, fellow competitor Marc Hensby had a driving accuracy percentage of 62.7%, just one percentage point less, yet Hensby’s rank of 102nd was 21 ranks below that of the rank given to Justin Rose.
Summary
The proposed method for ranking golfers according to their Total Driving skill takes into account the magnitude of the differences that exist between players on each of the two driving dimensions. The current PGA Tour method does not. The proposed method also takes into account the strong negative relationship that exists between driving accuracy and driving distance. This negative relationship is reflected in the new conditional standardized z-score. As a result, this new method gives a better overall reflection of the true Total Driving performance of PGA Tour golfers than does the current ranking system. Computationally, the proposed method is slightly more involved than other existing methods, but this is not a significant factor today.
It should be noted that this methodology can be applied in other areas in which an overall ranking is desired based on two correlated factors, which have different units of measurement and thus need to be combined in some way to provide an overall ranking.
References
Belkin, D.S., Gansneder, B., Pickens, M., Rotella, R. J., & Striegel, D. (1994) “Predictability and stability of Professional Golf Association tour statistics.” Perceptual and Motor Skills, 78, 1275-1280.
Callan, S. J. & Thomas, J. M. (2004) “Determinants of success among amateur golfers: An examination of NCAA Division I male golfers.” The Sports Journal 7, 3 at http://www.thesportjournal.org/2004Journal/Vol7-No3/CallanThomas.asp.
Callan, S. J. & Thomas, J. M. (2006) “Gender, skill and performance in amateur golf: An examination of NCAA Division I golfers.” The Sports Journal 8, 2 at http://www.thesportjournal.org/2006Journal/Vol9-No3/Callan.asp.
Dorsel, T.N., & Rotunda, R. J. (2001) “Low scores, Top 10 finishes and big money: An analysis of Professional Golf Association Tour statistics and how these relate to overall performance.” Perceptual and Motor Skills, 92, 575-585.
Engelhardt, G. M. (1997) “Differences in shot-making skills among high and low money winners on the PGA Tour.” Perceptual and Motor Skills, 84, 1314.
Engelhardt, G. M. (2002) “Driving distance and driving accuracy equals total driving:Reply to Dorsel and Rotunda.” Perceptual and Motor Skills 95, 423-424.
Shmanske, S. (2000) “Gender, skill and earnings in Professional Golf.” Journal of Sports Economics 1(4), 385-400.
Wiseman, F. and Chatterjee, S. (2006) “A comprehensive analysis of golf performance on the PGA Tour: 1990-2004.” Perceptual and Motor Skills, 102, 109-117.
TABLE 1
Driving Distance and Driving Accuracy: 1990-2005
| Year | Average Driving distance (yds.) |
Driving accuracy percentage |
Correlation between distance and accuracy |
|---|---|---|---|
| 1990 | 262.7 | 65.3% | -.359 |
| 1991 | 261.4 | 67.1% | -.306 |
| 1992 | 260.4 | 68.6% | -.416 |
| 1993 | 260.2 | 68.8% | -.417 |
| 1994 | 261.9 | 69.2% | -.346 |
| 1995 | 263.4 | 69.5% | -.457 |
| 1996 | 266.4 | 68.3% | -.469 |
| 1997 | 267.6 | 68.6% | -.448 |
| 1998 | 270.5 | 69.5% | -.469 |
| 1999 | 272.5 | 68.4% | -.471 |
| 2000 | 273.2 | 68.3% | -.379 |
| 2001 | 279.4 | 68.4% | -.346 |
| 2002 | 279.8 | 67.7% | -.474 |
| 2003 | 286.6 | 66.1% | -.612 |
| 2004 | 287.2 | 64.1% | -.606 |
| 2005 | 288.6 | 62.8% | -.679 |
Table 2
Revised 2005 PGA Tour Rankings for Total Driving (Top 40 players)
| Player | Driving Distance (yards) |
Driving Accuracy (%) |
Expected Driving Accuracy (%) |
ZDD | ZDA|DD | ZSUM | Rank | PGA Rank |
|---|---|---|---|---|---|---|---|---|
| Woods | 316.1 | 54.6 | 52.1 | 2.95 | 0.63 | 3.58 | 1 | 83 |
| Perry | 304.7 | 63.4 | 56.6 | 1.73 | 1.75 | 3.48 | 2 | 2 |
| Gutschewski | 310.5 | 57.9 | 54.3 | 2.35 | 0.92 | 3.27 | 3 | 54 |
| Wetterich | 311.7 | 56.6 | 53.8 | 2.48 | 0.70 | 3.18 | 4 | 73 |
| Hearn | 295.2 | 68.5 | 60.2 | 0.71 | 2.11 | 2.82 | 5 | 1 |
| Gronberg | 301.4 | 63.2 | 57.8 | 1.37 | 1.37 | 2.74 | 6 | 6 |
| Frazar | 301.0 | 63.5 | 58.0 | 1.33 | 1.41 | 2.74 | 7 | 3 |
| Warren | 299.2 | 64.2 | 58.7 | 1.14 | 1.41 | 2.55 | 8 | 3 |
| Glover | 302.2 | 60.7 | 57.5 | 1.46 | 0.81 | 2.27 | 9 | 26 |
| MacKenzie | 300.2 | 62.1 | 58.3 | 1.24 | 0.97 | 2.22 | 10 | 11 |
| Love III | 305.4 | 57.9 | 56.3 | 1.80 | 0.41 | 2.21 | 11 | 59 |
| Garcia | 303.5 | 59.4 | 57.0 | 1.60 | 0.61 | 2.21 | 12 | 38 |
| Durant | 289.2 | 70.9 | 62.6 | 0.06 | 2.13 | 2.20 | 13 | 5 |
| O’Hair | 300.1 | 61.4 | 58.3 | 1.23 | 0.78 | 2.02 | 14 | 26 |
| Singh | 301.1 | 60.2 | 58.0 | 1.34 | 0.57 | 1.92 | 15 | 38 |
| Long | 298.3 | 62.4 | 59.0 | 1.04 | 0.86 | 1.90 | 16 | 13 |
| Smith | 300.8 | 60.2 | 58.1 | 1.31 | 0.54 | 1.85 | 17 | 44 |
| Hend | 318.9 | 45.4 | 51.1 | 3.25 | -1.45 | 1.890 | 18 | 107 |
| Hughes | 291.3 | 67.5 | 61.8 | 0.29 | 1.47 | 1.76 | 19 | 7 |
| Stadler | 300.1 | 60.4 | 58.3 | 1.23 | 0.53 | 1.76 | 20 | 50 |
| Allenby | 297.7 | 62.3 | 59.3 | 0.98 | 0.77 | 1.75 | 21 | 20 |
| Mayfair | 288.2 | 69.8 | 63.0 | -0.04 | 1.75 | 1.71 | 22 | 9 |
| Appleby | 300.6 | 59.3 | 58.1 | 1.29 | 0.29 | 1.58 | 23 | 61 |
| Snyder III | 291.8 | 66.3 | 61.6 | 0.34 | 1.21 | 1.56 | 24 | 8 |
| Purdy | 295.2 | 63.4 | 60.2 | 0.71 | 0.81 | 1.52 | 25 | 15 |
| Brigman | 295.5 | 63.1 | 60.1 | 0.74 | 0.76 | 1.50 | 26 | 18 |
| Bryant | 283.2 | 73.0 | 64.9 | -0.58 | 2.07 | 1.49 | 27 | 30 |
| Rollins | 294.4 | 63.7 | 60.6 | 0.62 | 0.81 | 1.43 | 28 | 10 |
| Jobe | 302.3 | 57.3 | 57.5 | 1.47 | -0.05 | 1.42 | 29 | 82 |
| Brehaut | 286.6 | 69.9 | 63.6 | -0.21 | 1.62 | 1.40 | 30 | 17 |
| Ogilvy | 298.0 | 60.7 | 59.2 | 1.01 | 0.39 | 1.40 | 31 | 54 |
| Henry | 297.6 | 61.0 | 59.3 | 0.97 | 0.43 | 1.40 | 32 | 44 |
| Rose | 294.1 | 63.7 | 60.7 | 0.59 | 0.78 | 1.37 | 33 | 13 |
| Westwood | 296.8 | 61.5 | 59.6 | 0.88 | 0.48 | 1.36 | 34 | 43 |
| Johnson | 290.0 | 66.9 | 62.3 | 0.15 | 1.19 | 1.34 | 35 | 15 |
| Senden | 291.0 | 66.0 | 61.9 | 0.26 | 1.06 | 1.31 | 36 | 11 |
| Mickelson | 300.0 | 58.7 | 58.4 | 1.22 | 0.08 | 1.30 | 37 | 77 |
| Watney | 298.9 | 59.4 | 58.8 | 1.11 | 0.15 | 1.26 | 38 | 68 |
| Trahan | 295.8 | 61.8 | 60.0 | 0.77 | 0.46 | 1.23 | 39 | 33 |
| Pappas | 309.4 | 50.6 | 54.7 | 2.23 | -1.06 | 1.17 | 40 | 109 |
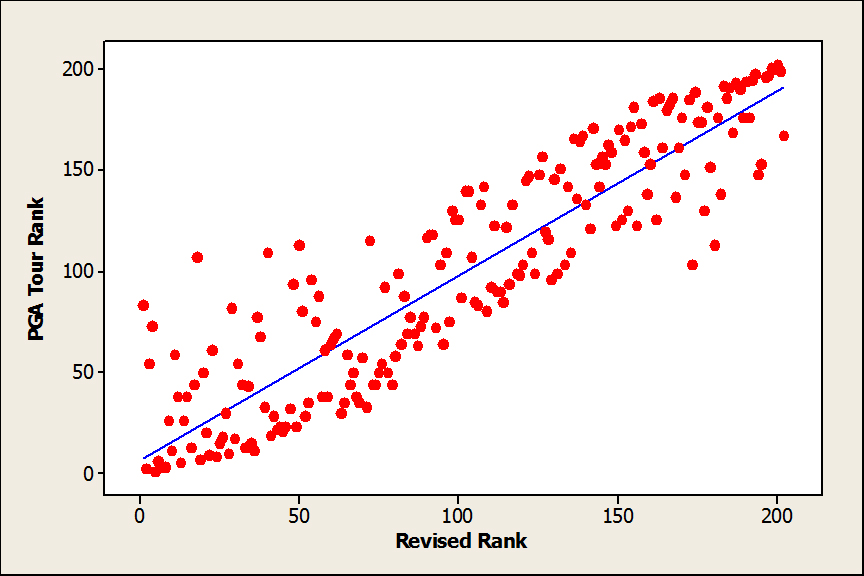
Figure 1.
Scatterplot of Revised Rankings Versus PGA Tour Rankings
